Map Coloring

This example solves a map-coloring problem to demonstrate using Ocean tools to solve a problem on a D-Wave system. It demonstrates using the D-Wave system to solve a more complex constraint satisfaction problem (CSP) than that solved in the example of Constrained Scheduling.

Constraint satisfaction problems require that all a problem’s variables be assigned values, out of a finite domain, that result in the satisfying of all constraints. The map-coloring CSP, for example, is to assign a color to each region of a map such that any two regions sharing a border have different colors.

Coloring a map of Canada with four colors.

The constraints for the map-coloring problem can be expressed as follows:

• Each region is assigned one color only, of \(C\) possible colors.
• The color assigned to one region cannot be assigned to adjacent regions.

Example Requirements

To run the code in this example, the following is required.

• The requisite information for problem submission through SAPI, as described in Using a D-Wave System.
• Ocean tools dwavebinarycsp and dwave-system. For graphics, you will also need NetworkX.

If you installed dwave-ocean-sdk and ran dwave config create, your installation should meet these requirements.

Solution Steps

Following the standard solution process described in Section Solving Problems on a D-Wave System, we (1) formulate the problem as a binary quadratic model (BQM) by using unary encoding to represent the \(C\) colors: each region is represented by \(C\) variables, one for each possible color, which is set to value \(1\) if selected, while the remaining \(C-1\) variables are \(0\). (2) Solve the BQM with a D-Wave system as the sampler.

The full workflow is as follows:

1. Formulate the problem as a graph, with provinces represented as nodes and shared borders as edges, using 4 binary variables (one per color) for each province.
2. Create a binary constraint satisfaction problem and add all the needed constraints.
3. Convert to a binary quadratic model.
4. Sample.
5. Plot a valid solution.

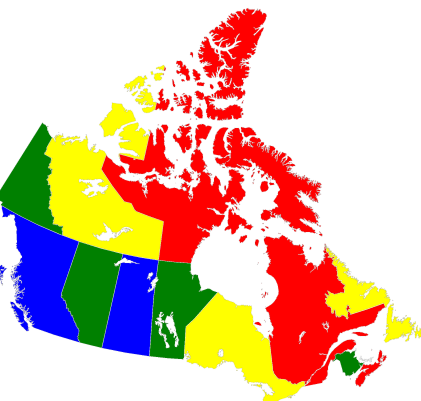
Four-Color Canadian Map

This example finds a solution to the map-coloring problem for a map of Canada using four colors (the sample code can easily be modified to change the number of colors or use different maps). Canada’s 13 provinces are denoted by postal codes:

Canadian Provinces’ Postal Codes

Code	Province	Code	Province
AB	Alberta	BC	British Columbia
MB	Manitoba	NB	New Brunswick
NL	Newfoundland and Labrador	NS	Nova Scotia
NT	Northwest Territories	NU	Nunavut
ON	Ontario	PE	Prince Edward Island
QC	Quebec	SK	Saskatchewan
YT	Yukon

Note

You can skip directly to the complete code for the problem here: Map Coloring: Full Code.

The example uses the D-Wave binary CSP tool to set up constraints and convert the CSP to a binary quadratic model, dwave-system to set up a D-Wave system as the sampler, and NetworkX to plot results.

import dwavebinarycsp
from dwave.system.samplers import DWaveSampler
from dwave.system.composites import EmbeddingComposite
import networkx as nx
import matplotlib.pyplot as plt

Start by formulating the problem as a graph of the map with provinces as nodes and shared borders between provinces as edges (e.g., “(‘AB’, ‘BC’)” is an edge representing the shared border between British Columbia and Alberta).

# Represent the map as the nodes and edges of a graph
provinces = ['AB', 'BC', 'MB', 'NB', 'NL', 'NS', 'NT', 'NU', 'ON', 'PE',
             'QC', 'SK', 'YT']
neighbors = [('AB', 'BC'), ('AB', 'NT'), ('AB', 'SK'), ('BC', 'NT'), ('BC', 'YT'),
             ('MB', 'NU'), ('MB', 'ON'), ('MB', 'SK'), ('NB', 'NS'), ('NB', 'QC'),
             ('NL', 'QC'), ('NT', 'NU'), ('NT', 'SK'), ('NT', 'YT'), ('ON', 'QC')]

Create a binary constraint satisfaction problem based on two types of constraints, where csp is the dwavebinarycsp CSP object:

• csp.add_constraint(one_color_configurations, variables) represents the constraint that each node (province) select a single color, as represented by valid configurations one_color_configurations = {(0, 0, 0, 1), (0, 0, 1, 0), (0, 1, 0, 0), (1, 0, 0, 0)}
• csp.add_constraint(not_both_1, variables) represents the constraint that two nodes (provinces) with a shared edge (border) not both select the same color.

# Function for the constraint that two nodes with a shared edge not both select
# one color
def not_both_1(v, u):
    return not (v and u)

# Valid configurations for the constraint that each node select a single color
one_color_configurations = {(0, 0, 0, 1), (0, 0, 1, 0), (0, 1, 0, 0), (1, 0, 0, 0)}
colors = len(one_color_configurations)

# Create a binary constraint satisfaction problem
csp = dwavebinarycsp.ConstraintSatisfactionProblem(dwavebinarycsp.BINARY)

# Add constraint that each node (province) select a single color
for province in provinces:
    variables = [province+str(i) for i in range(colors)]
    csp.add_constraint(one_color_configurations, variables)

# Add constraint that each pair of nodes with a shared edge not both select one color
for neighbor in neighbors:
    v, u = neighbor
    for i in range(colors):
        variables = [v+str(i), u+str(i)]
        csp.add_constraint(not_both_1, variables)

Convert the CSP into a binary quadratic model so it can be solved on the D-Wave system.

bqm = dwavebinarycsp.stitch(csp)

The next code sets up a D-Wave system as the sampler and requests 50 samples.

Note

In the code below, replace sampler parameters as needed. If you configured a default solver, as described in Using a D-Wave System, you should be able to set the sampler without parameters as sampler = EmbeddingComposite(DWaveSampler()). You can see this information by running dwave config inspect in your terminal.

# Sample 50 times
sampler = EmbeddingComposite(DWaveSampler(endpoint='https://URL_to_my_D-Wave_system/', token='ABC-123456789012345678901234567890', solver='My_D-Wave_Solver'))
response = sampler.sample(bqm, num_reads=50)

Note

The next code requires Matplotlib.

Plot a valid solution.

# Function that plots a returned sample
def plot_map(sample):
    G = nx.Graph()
    G.add_nodes_from(provinces)
    G.add_edges_from(neighbors)
    # Translate from binary to integer color representation
    color_map = {}
    for province in provinces:
          for i in range(colors):
            if sample[province+str(i)]:
                color_map[province] = i
    # Plot the sample with color-coded nodes
    node_colors = [color_map.get(node) for node in G.nodes()]
    nx.draw_circular(G, with_labels=True, node_color=node_colors, node_size=3000, cmap=plt.cm.rainbow)
    plt.show()

# Plot the lowest-energy sample if it meets the constraints
sample = next(response.samples())
if not csp.check(sample):
    print("Failed to color map")
else:
    plot_map(sample)

The plot shows a solution returned by the D-Wave solver. No provinces sharing a border have the same color.

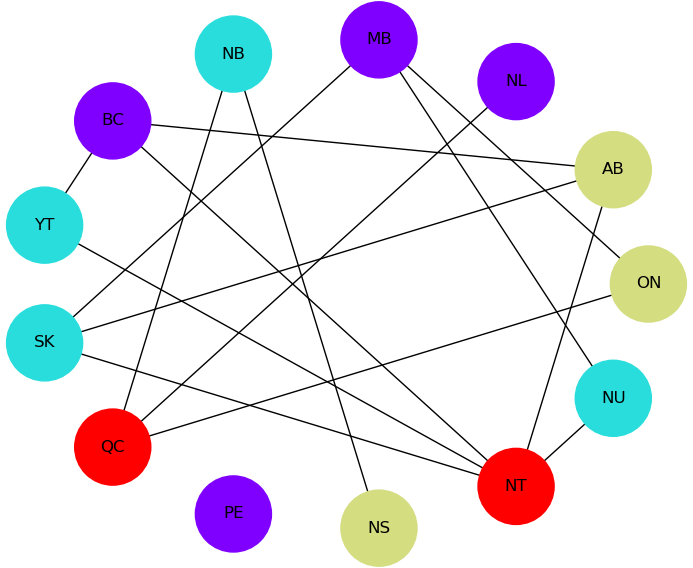
Solution for a map of Canada with four colors. The graph comprises 13 nodes representing provinces connected by edges representing shared borders. No two nodes connected by an edge share a color.

Note

You can copy the complete code for the problem here: Map Coloring: Full Code.